header ads

FISIKA

http://verajelajah.blogspot.com/ Desember 04, 2018

Gerak Parabola

      Gerak parabola digambarkan dengan lintasan melengkung, menyerupai setengah lingkaran. Melalui halaman ini, akan diulas definisi gerak parabola sampai rumus gerak parabola dan keterangannya. Pada bagian akhir akan diberikan contoh soal gerak parabola dan pembahasannya.
      
      Penyajian gerak parabola biasa diberikan pada bidang koordinat. Sehingga, lintasan parabola yang berupa lengkungan dapat diurai dalam vektor. Sumbu y mewakili gerak lurus berubah beraturan (GLBB). Sedangkan sumbu x mewakili gerak lurus beraturan (GLB).

Definisi Gerak Parabola

Gerak parabola atau yang biasa disebut dengan gerak peluru dapat dikatakan sebagai gabungan antara gerak lurus beraturan (GLB) dan gerak lurus berubah beraturan (GLBB). Seperti yang sudah disinggung sebelumnya bahwa sumbu x mewakili gerak GLB dan sumbu y mewakili gerak GLBB.
Lintasan yang dilalui pada gerak parabola termasuk dalam bidang dua dimensi. Gerak parabola dari suatu benda membentuk sudut elevasi dengan sumbu x atau sumbu y. Walaupun terdiri dari dua komposisi gerak, namun kedua gerak ini tidak saling memengaruhi.
Gambar lintasan gerak parabola dan keterangannya dapat dilihat seperti berikut.
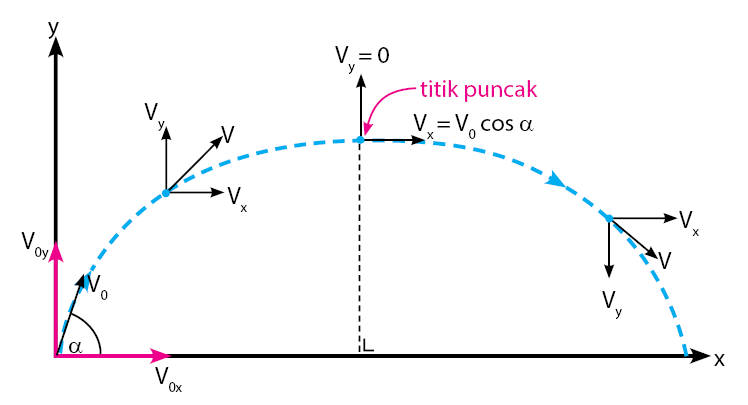
gerak parabola dan keterangannya
Kecepatan awal terhadap arah horizontal (sumbu x)
  \[ V_{0x} = V_{0} \cdot cos \; \alpha \]
  \[ V_{0x} = 100 \frac{4}{5} \]
  \[ V_{0x} = 80 \; m/s \]
Kecepatan awal terhadap arah vertikal (sumbu y)
  \[ V_{0y} = V_{0} \; sin \; \alpha \]
  \[ V_{0y} = 100 \cdot \frac{3}{5} \]
  \[ V_{0y} = 60 \; m/s \]
Waktu yang diperlukan peluru untuk mencapai titik tertinggi
  \[ t_{p} = \frac{V_{0} \cdot sin \; \alpha}{g} \]
  \[ t_{p} = \frac{100 \cdot sin \; 37^{0}}{10} \]
  \[ t_{p} = \frac{100 \cdot \frac{3}{5} }{10} \]
  \[ t_{p} = 6 \; \textrm{detik} \]
Kecepatan peluru saat mencapai titik tertinggi
Arah vertikal
  \[ V_{y} = 0 \]
Arah Horizontal
  \[ V_{x} = V_{0} \cdot cos \alpha \]
  \[ V_{x} = 100 \cdot \frac{4}{5} = 80 \; m/s \]
Tinggi maksimum yang bisa dicapai peluru (y_{max})
  \[ y_{max} = \frac{V_{0}^{2} \cdot sin^{2} \alpha}{2g} \]
\[ y_{max} = \frac{100^{2} \cdot \left( \frac{3}{5} \right)^{2} }{2 \cdot 10} \]
  \[ y_{max} = \frac{10.000 \times \frac{9}{25} }{20} \]
  \[ y_{max} = \frac{3.600}{20} \]
  \[ y_{max} = 1.800 \; \textrm{meter} \]
Waktu yang diperlukan peluru untuk mencapai sasaran (jarak terjauh arah mendatar)
Waktu untuk mencapai jarak mendatar paling jauh adalah dua kali waktu untuk mencapai ketinggian maksimum, yaitu 2 \times 6 = 12 sekon.
Jarak terjauh yang dicapai peluru (x_{max})
Dapat diperoleh menggunakan rumus
  \[ x_{max} = V_{0}t \cdot cos \; \alpha \]
Karena sudah sudah diketahui waktu untuk mencapai jarak maksimum, yaitu 12 sekon.
  \[ x_{max} = V_{0}t \cdot cos \; \alpha \]
  \[ x_{max} = 100 \cdot 12 \cdot \frac{4}{5} \]
  \[ x_{max} = 960 \; \textrm{meter} \]

Tags:

Posting Komentar

0 Komentar